Solve the inequality 3b-7 32 – In the realm of mathematics, inequalities reign supreme, and among them, the inequality 3b – 7 > 32 stands out as a captivating puzzle. Join us as we embark on a journey to unravel its secrets, unraveling the steps to its solution and exploring its practical applications.

Delving into the world of inequalities, we’ll uncover the different types and their significance. We’ll then turn our attention to the inequality 3b – 7 > 32, breaking it down step by step to isolate the variable b and find its solution.

Inequality Overview

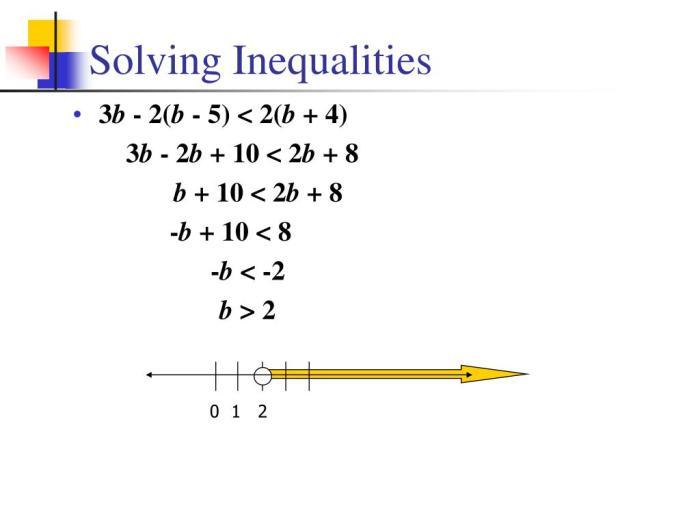
Inequalities are mathematical statements that compare two expressions and determine whether they are equal or not. They are used to represent relationships between variables and to solve problems in various fields, such as algebra, geometry, and economics.

There are different types of inequalities, each with its own symbol:

• Less than (<):The left expression is smaller than the right expression.
• Greater than (>):The left expression is larger than the right expression.
• Less than or equal to (≤):The left expression is smaller than or equal to the right expression.
• Greater than or equal to (≥):The left expression is larger than or equal to the right expression.

The Inequality 3b

7 > 32

The inequality 3b – 7 > 32 is an example of a greater than inequality. It means that the expression 3b – 7 is greater than the number 32.

Solving the Inequality

To solve the inequality 3b – 7 > 32, we need to isolate the variable bon one side of the inequality sign.

Isolating the Variable b

1. Add 7 to both sides of the inequality:

• b
• 7 + 7 > 32 + 7

Simplifying:

b > 39

2. Divide both sides of the inequality by 3:

(3b) / 3 > 39 / 3

Simplifying:

b> 13

Therefore, the solution to the inequality 3b – 7 > 32 is b> 13.

Applications of the Inequality

Solving inequalities extends beyond mathematical equations and has practical applications in various real-world scenarios. Understanding the solution to 3b – 7 > 32 can be valuable in practical situations.

Business and Finance

• Inventory Management:A retail store needs to determine the minimum number of products they must stock to meet customer demand. By setting up an inequality like 3b – 7 > 32, where b represents the number of products, they can ensure they have sufficient inventory to avoid stockouts.

• Investment Returns:An investor wants to calculate the minimum return on investment (ROI) required to cover their expenses. Using the inequality 3b – 7 > 32, where b represents the ROI, they can determine the minimum acceptable return rate.

Science and Engineering

• Chemical Reactions:In chemistry, the concentration of reactants and products is often represented by inequalities. For example, 3b – 7 > 32 could represent the minimum concentration of a reactant required for a reaction to occur.
• Structural Design:Engineers use inequalities to determine the maximum load a structure can withstand. By setting up an inequality like 3b – 7 > 32, where b represents the load, they can ensure the structure is safe under expected conditions.

Extensions of the Inequality: Solve The Inequality 3b-7 32

The inequality 3b – 7 > 32 can be extended and modified in various ways to explore different mathematical concepts and applications.

If you’re feeling stumped on solving the inequality 3b-7 32, check out the wordly wise book 5 lesson 1 for some helpful tips. It provides a clear explanation of the steps involved in solving inequalities, which can be applied to 3b-7 32. So, if you’re ready to conquer this inequality, dive into the lesson and get started!

Generalization

The inequality 3b – 7 > 32 can be generalized to the form ax + b > c, where a, b, and c are constants. This generalized inequality represents a linear inequality that can be solved using the same principles as the original inequality.

Variations

The inequality 3b – 7 > 32 can be modified by changing the inequality sign. For example, the inequality 3b – 7< 32 represents a different set of solutions. Additionally, the constants in the inequality can be changed to create new inequalities with different solutions.

Examples

• Solve the inequality 2x + 5 > 15.
• Solve the inequality 5 – 3y< 10.
• Solve the inequality 4z – 10 > 2z + 15.

Related Concepts

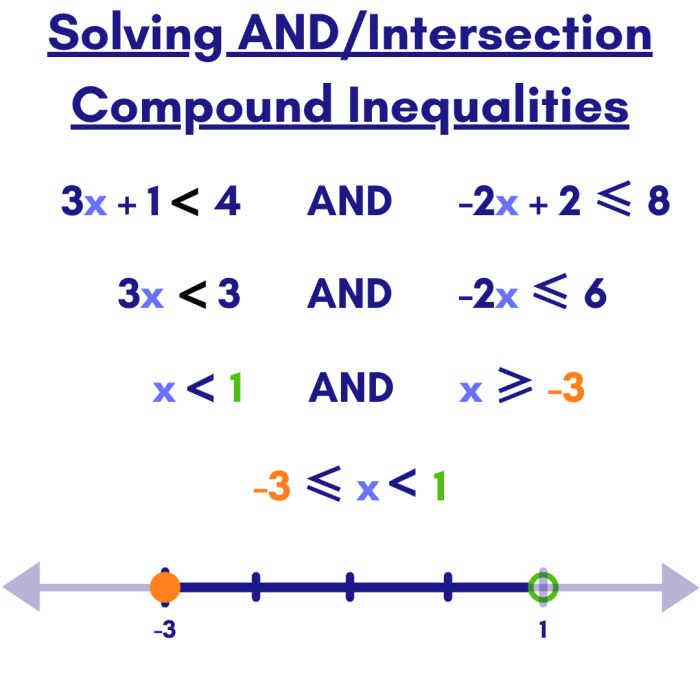
Inequalities are closely connected to various mathematical concepts, enriching our understanding and problem-solving abilities. Let’s explore how the inequality 3b – 7 > 32 interacts with these related concepts.

Linear Equations

Linear equations are equations of the form ax + b = c, where a, b, and c are constants and x is the variable. Solving linear equations involves finding the value of x that makes the equation true. The inequality 3b – 7 > 32 can be transformed into a linear equation by subtracting 32 from both sides, resulting in 3b > 25.

Absolute Value Inequalities, Solve the inequality 3b-7 32

Absolute value inequalities involve expressions with absolute values, such as |x| < 5. Solving absolute value inequalities requires considering both positive and negative values of the variable. The inequality 3b - 7 > 32 can be rewritten as |3b- 39| > 25, where the absolute value ensures that the expression is positive.

Compound Inequalities

Compound inequalities are inequalities that combine multiple inequalities using conjunctions like “and” or disjunctions like “or.” For example, the inequality (3b – 7 > 32) and (b< 10) is a compound inequality that represents the intersection of the two inequalities.

Common Queries

What is the first step in solving the inequality 3b- 7 > 32?

Add 7 to both sides of the inequality.

How can I apply the solution to 3b- 7 > 32 in real life?

The solution can be used to determine the range of values for b that satisfy a given condition in practical situations.