Proving that a quadrilateral is a parallelogram worksheet – Proving that a quadrilateral is a parallelogram is a fundamental concept in geometry. This worksheet provides a comprehensive overview of the different methods for proving that a quadrilateral is a parallelogram, including using angle properties, side properties, and diagonal properties.
By understanding the properties of parallelograms and the different methods for proving that a quadrilateral is a parallelogram, students will be able to solve a variety of problems involving parallelograms.
Defining a Parallelogram
A parallelogram is a quadrilateral with two pairs of parallel sides. This means that the opposite sides of a parallelogram are parallel and equal in length. Parallelograms are a type of quadrilateral, which is a polygon with four sides.
The properties of a parallelogram include:
- Opposite sides are parallel and equal in length.
- Opposite angles are equal in measure.
- Consecutive angles are supplementary (add up to 180 degrees).
- The diagonals of a parallelogram bisect each other.
Examples of parallelograms include squares, rectangles, and rhombuses.
Proving a Quadrilateral is a Parallelogram: Proving That A Quadrilateral Is A Parallelogram Worksheet

There are several different methods for proving that a quadrilateral is a parallelogram. These methods include:
- Using angle properties
- Using side properties
- Using diagonal properties
To apply these methods, you can use the following steps:
- Identify the given information about the quadrilateral.
- Choose a method for proving that the quadrilateral is a parallelogram.
- Apply the method to the given information.
- Write a conclusion stating whether or not the quadrilateral is a parallelogram.
Using Angle Properties, Proving that a quadrilateral is a parallelogram worksheet
One way to prove that a quadrilateral is a parallelogram is to use its angle properties. The angle properties of a parallelogram are as follows:
- Opposite angles are equal in measure.
- Consecutive angles are supplementary (add up to 180 degrees).
To prove that a quadrilateral is a parallelogram using its angle properties, you can use the following steps:
- Measure the angles of the quadrilateral.
- Check if the opposite angles are equal in measure.
- Check if the consecutive angles are supplementary.
- If both of these conditions are met, then the quadrilateral is a parallelogram.
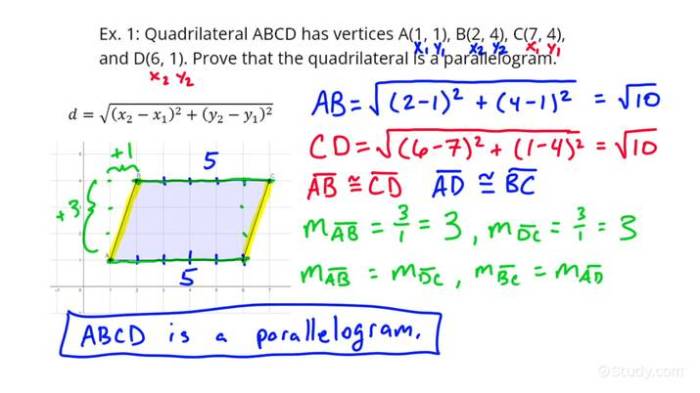
Using Side Properties
Another way to prove that a quadrilateral is a parallelogram is to use its side properties. The side properties of a parallelogram are as follows:
- Opposite sides are parallel and equal in length.
To prove that a quadrilateral is a parallelogram using its side properties, you can use the following steps:
- Measure the sides of the quadrilateral.
- Check if the opposite sides are equal in length.
- Check if the opposite sides are parallel.
- If both of these conditions are met, then the quadrilateral is a parallelogram.
Using Diagonal Properties
A third way to prove that a quadrilateral is a parallelogram is to use its diagonal properties. The diagonal properties of a parallelogram are as follows:
- The diagonals of a parallelogram bisect each other.
To prove that a quadrilateral is a parallelogram using its diagonal properties, you can use the following steps:
- Draw the diagonals of the quadrilateral.
- Check if the diagonals bisect each other.
- If the diagonals bisect each other, then the quadrilateral is a parallelogram.
Essential Questionnaire
What is a parallelogram?
A parallelogram is a quadrilateral with two pairs of parallel sides.
What are the properties of a parallelogram?
The properties of a parallelogram include:
- Opposite sides are parallel.
- Opposite sides are congruent.
- Opposite angles are congruent.
- Diagonals bisect each other.
How can you prove that a quadrilateral is a parallelogram?
There are several different methods for proving that a quadrilateral is a parallelogram, including:
- Using angle properties
- Using side properties
- Using diagonal properties